As an audio engineer, you might decide to work with two or more microphones in order to generate an alternative tonal option for a source or else you might want to pick up a partial portion of the sound from the source. When you eventually decide to combine the multiple options and to sum them into a bus or a whole mix, you are exposing the sound of your recording to the risk of so called "comb filtering" due to incorrect phase. That means the mix might suffer a lack of bass content, or become "boxy" or "phony," and sound definitely weird. While you won't hear these effects if you spread the sounds across the stereo image as i nthat configuration the signals are only partially summed, as soon as you (or someone else) listen in mono the problems become strikingly relevant.

What's going on? Why does the sound change? Well...the sum of two (or more) signals don't always give a positive result: it can also give a negative result. To be perfectly correct: a null result. Sound waves consist of peaks and dips in pressure: if a given sound wave arrives at mic #2 with such a delay that its "peak" corresponds to a "dip" picked up by mic #1, the net result is zero.

It's common practice to position microphones very close to each other in order to avoid the delay. Or else, one can follow the 1:3 rule: position the second mic at a distance at least three times the distance from the source to the first mic. Is it a matter of time? Well... yes. And no. Not only time, but also...

When dealing with phase, we first must be aware of some facts regarding A) the physical nature of sound and B) the way microphones work. I was not totally aware of these facts until I found myself dealing with phase issues and decided to understand them. Admittedly, this was not an easy task. I found these facts to be somehow hidden within the dedicated literature, inaccurately described or else misrepresented in different ways, and sometimes completely ignored. What follows is the result of a personal research both theoretical and practical in the use of two or more microphones. 

The first fact to be aware of you might already know: phase is frequency-dependant.

There is no such thing as a "general phase problem" pertaining to a combination of signals generated by multiple microphones. For a given combination, a phase problem always occurs at a certain fundamental frequency and at higher, mathematically related, frequencies (depending on the type of microphones used). As previously said, sound waves have peaks and dips of pressure: physical space (distance) between them measures differently for each frequency because each frequency has its own wavelength. In the example above, when a peak at the second microphone corresponds to a dip at the first microphone, the result is a total cancellation of one fundamental frequency (plus higher frequencies). But in any case like this, there will be a different wavelength (i.e. frequency) for which both microphones simultaneously pick up a peak (or a dip), and the result is an increase in volume for that frequency. In other words, any time there is cancellation at one fundamental frequency, there will be a boost at another fundamental frequency.

This is very important to be aware of: phase is always a risk and — at the same time — an opportunity to carve a desired tonal shape using your main recording tools: the microphones. Frequencies are canceled while frequencies are enhanced.

There is a second fact we must be aware of: microphones don't translate sound pressure in the same way. No, I am not talking about different frequency responses. Maybe you know this as well, but are you sure you know the whole story? 

The types of microphones widely used nowadays are condensers, dynamics, and ribbons. 

In a condenser microphone, the transducing element, called a capsule, consists of a supporting ring to which are attached an extremely thin, circular sheet of metal-sputtered plastic material under tension, called a diaphragm, and a thicker, fixed, perforated metallic plate behind that (if you follow the direction of sound wave). (In the majority of condenser capsules in use today, two diaphragms are present, one on each side of the backplate. For the purpose of this explanation we can just consider the front one.)

The two elements, diaphragm and backplate, are separated by an air gap and are polarized by an electrical charge provided, effectively constituting the two arms of a capacitor (condenser is an old term for capacitor). The thin diaphragm involved in the periodic variation of air pressure of the sound wave vibrates together with it. With positive pressure, the diaphragm is pushed against the backplate, the distance between them shortens and so the capacitance of the system is varied. The other way around, the diaphragm is pulled by de-compression; the distance from the backplate increases and the capacitance of the system varies in the opposite verse. Said oscillation of the capacitance is electrically used to generate the variation of voltage at the output of the microphone. Note that the amplitude of the output signal is highest when the diaphragm is at its closest or farthest position from the backplate. Therefore in a condenser microphone the level of the signal is directly proportional to the air pressure: the more pressure (or de-pressure) the more signal.

With dynamic and ribbon mics, transduction of air pressure into electric voltage is accomplished using electromagnetic induction. Similarly to a condenser, also in dynamic microphones a diaphragm is present. The whole system though is heavier — i.e. slower and "less accurate" — because attached to the diaphragm is a coil of thin copper wire. Said coil of wire surrounds a fixed, strong magnet. According to the principles of electromagnetic induction, voltage is induced on the coil when it moves (remember: it's attached to the diaphragm) and interferes with the magnetic field emanated by the magnet.

Note that movement is the necessary condition for voltage to be induced on the coil: if no movement, then no output signal. Here the amplitude of the output signal is highest when the diaphragm is moving at its fastest speed. What you must understand is that the fastest speed of the diaphragm takes place exactly in between two opposite peaks of pressure, i.e. when there's no pressure on the diaphragm. This is exactly when the output of a condenser microphone is at zero. Therefore, in a dynamic microphone the level of the signal is inversely proportional to the air pressure: the more pressure (or de-pressure) the less signal.

Ribbon microphones operate in a similar fashion, also according to the principles of electromagnetism. A conductive metallic element as a very thin ribbon is kept under tension, free to oscillate in between the two poles of a magnet and connected to the output pins. Voltage is present at the output pins when the ribbon, hit by air pressure, moves within the magnetic field and in doing so gets voltage induced onto itself. Exactly like a dynamic capsule (the principle is the same), the movement of the ribbon is the necessary condition for voltage to be present at the output. And also in this case the output level is inversely proportional to the pressure on the diaphragm.

Okay, let's categorize dynamic and ribbon microphones as electromagnetic microphones.

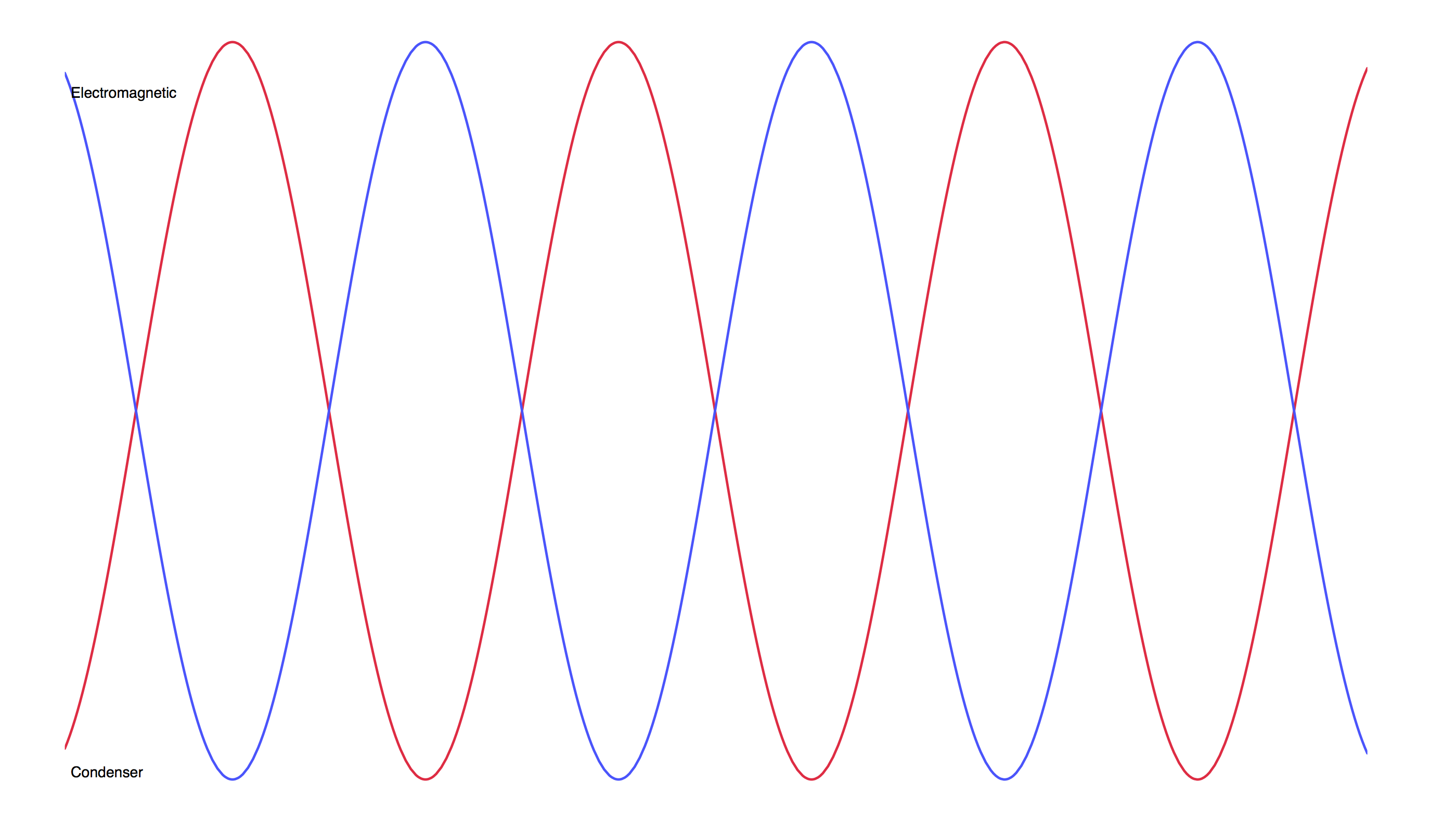
Following what's been said above, let's plot the output of a condenser microphone and the output of an electromagnetic microphone as the same sound pressure varies on their diaphragms: we'll obtain two resulting waveforms which are 90° out of phase. 

You can verify this by yourself: set up two microphones, one condenser and one dynamic (or ribbon) very close to each other, as coincident as possible, at a few inches from a P.A. speaker reproducing a single frequency, say a 100 Hz tone. Record on two different tracks the output of the mics (use preamps of the same brand/type). Assuming you are recording into a DAW, zoom in a lot and look very close at the two waveforms: you'll see that the electromagnetic precedes the condenser (look at the peaks): it picked up the same air pressure but translated that "earlier." The two output signals ARE NOT IN PHASE even though the two microphones are perfectly aligned in front of the speaker!

The plot provides very useful information about what to do next. Never forget that phase is frequency dependant! The plot tells you where to position microphones in order to tune them (i.e. obtain perfect phase) at a specific frequency you want to enhance or else get rid of. It tells you that if they transduce the same way (both electromagnetics or both condensers), you could position them as coincident as possible. It also tells you that if they transduce the different way, you should firmly avoid the "as coincident as possible" positioning. If for any given frequency, electromagnetic transduction "precedes" the capacitive one, the next thing to know is that you must place the condenser closer to the source, ahead of the electromagnetic in order to compensate for the phase shift. At what distance from the electromagnetic? How much should the two microphones be spaced apart? The plot says one quarter wavelength of the target frequency. 

Surprisingly, during my experiments I was never able to set up microphones exactly according to the plot. I don't know why yet, but I am studying the various cases. (A number of factors are under the lens: behavior of pressure as sound travels away from the source, changing its nature from spherical wave to plane wave; also room acoustics and internal impedance of microphones are being analyzed.)

Therefore it's been impossible to go non-empirical and just follow the 90° rule: it never worked so precisely. Still the condenser has to be placed closer to the source, but I have to go out in the field and search for the exact relative position where both microphones pick up a peak of pressure of the desired frequency. I think it's a great value to know the theory behind, whose basic principles remain confirmed (I'll tell later about an empirical method to find perfect phase for a frequency).

In many applications the electromagnetic is preferred closer to the source. The plot tells you what to do:

You'd have to place the condenser at one quarter wavelength after the electromagnetic and invert the phase of its signal. That's because you're actually placing the condenser at half wavelength from its in-phase position and after one half wavelength pressure has phase reversed. Got that?

What if you want to use two electromagnetics, like one dynamic and one ribbon? Well... they transduce air pressure in the same way so there's no phase difference. Place the two as coincident as possible. Or place them spaced apart one full wavelength. "But... wait a minute: that's almost 14 feet for 80 Hz!!!" you might say. Uh... You're right. Is your room smaller than that? Okay, place the farthest mic at half wavelength and press the phase/polarity button on your mic preamp: pressure is 180° out of phase at half wavelength. You're at 7 feet now.

What the plot says is that if you're looking for perfect phase between microphones you should place them according to this pattern (following the direction of sound propagation):

ELECTROMAGNETIC — PHASE REVERSED CONDENSER — PHASE REVERSED ELECTROMAGNETIC — CONDENSER

First of all make a decision about which frequency you want to tune your microphones at (how about a fundamental?). Then choose your first microphone and follow the pattern. One can also think the other way around, looking for a total out-of-phase cancellation. Why not? You might be able to tame a certain annoying frequency. With some practice, you'll find the phase reversal button on your preamps to be a really great feature and to make a lot more sense now. Find the perfect phase and press that button: frequency canceled!

Is your room smaller than 7 feet? No problem: you can always go hybrid very easily, if you're working with a DAW, by moving tracks along the timeline.

Is your room a sufficiently large one? Following the rule might lead to sonically non-ideal setups. Say you want to tune at 80 Hz your close bass drum dynamic and the ribbon you're using in front of the kit. They are both electromagnetic microphones: as seen before, tuning distance is half wavelength with polarity reversed on the ribbon. Which is the distance? Speed of sound over frequency gives you full wavelength: 340/80 = 4.25 meters (13.94 feet). Divide that by 2 and you find that the ribbon element should be placed at 2.125 meters (6.97 feet) from the dynamic capsule. And don't forget to invert the phase. 80 Hz are in tune, bass drum sounds great by the way, but... "Mmmh, the sound of the ribbon mic is just too roomy: the balance between direct and ambient sound is not a good one in that position". Okay. Still, you can reposition it where it sounded best, and after recording the good take you can nudge back on the timeline the ribbon track to where the 80 Hz are in phase (since the ribbon provides me with a more "global" sound of the drum kit, I'd rather pull ahead the close, dynamic mic: it's such a subtle move that it won't ruin the timing of the performance. Nevertheless inform the drummer about your operation).

Low frequencies are the most susceptible to degradation caused by phase issues and that's the reason why tuned mic'ing greatly improves the tone in the lower end of the audio spectrum. Here follows an explanation of what I do in some situations concerning low frequencies: bass drum, electric guitar, electric bass guitar or baritone guitar.

I use a speaker cabinet with the 15" woofer placed accurately to mimic the position of the bass drum batter head, so that the woofer is as close to the dynamic mic (which I normally use for close mic'ing the bass drum) as the head will be. Then I position the ribbon capsule at about 1.20/1.40 meters (about 4 feet), depending on the kit size and the drummer's power. I flip the phase on the ribbon's preamp. I send alternatively three tones to the speaker: 50 Hz, 63 Hz, and 80 Hz. I record a few seconds of each and then nudge one of the tracks of the exact number of samples, which separate the peaks of one from the other. As the plot suggests, the dynamic needs to be anticipated in order to be tuned with the ribbon at said frequencies: more at 50 Hz, less at 63 Hz, even less at 80 Hz (wavelength shortens as frequency raises). I write down the three values. When I am done recording I have the options to precisely tune the two bass drum sounds to three alternative frequencies (or any other simply by nudging at different positions in between), greatly improving the low end content of the bass drum itself and the whole kit. Pretty cool. I also find that it's a lot easier to blend in the close mic to the overall sound as picked up by the ribbon microphone.

I follow a very similar approach when dealing with an amp cabinet of an electric guitar: setting up a dynamic and either a ribbon almost coincident or a condenser with phase reversed. Tuning them at a certain low frequency (or more than one alternatively), allows me to boost or cancel that frequency depending on the situation (part, song, musical genre).

A different situation I deal with following the same basic principles: the sound of an electric bass picked up by a (usually) dynamic microphone at the speaker cabinet and by a D.I. box. I send a 40 Hz tone to the D.I. and the linked amp. Again I record a few seconds and then count the samples, which separate the peaks: here the D.I. channel is the one that usually gets delayed. After the bass player has completed his/her performance, I'll nudge back the D.I. track to eventually get a really deep tone from the combination of the two tracks. And like in the bass drum case, mixing the two is a lot easier. I usually tune at 40 Hz but you might find that best results are obtained with a different frequency.

A quick, final note about the use of aligning algorithms (i.e. plug-ins). First of all I don't use them so I can't comment on results. I have watched over Internet videos showing how they look and how to work with them. The results I heard in some cases were interesting to me, in other cases they were not. I've heard talk about a "difference between time and phase" which doesn't make any sense to me. It's always hard for me to rely on a tool that I am not conscious about the way it functions. I strongly believe that it is the audio engineer's job to take care of phase issues and related: so either you are an audio engineer or you are not. And if you are, rest assured you can do an excellent job even without mysterious software. Sure it takes time and dedication. On top of that, please note that what I call tuned mic'ing is not about aligning. You could go ahead and align in time the hits of a bass drum or the notes of an electric bass but in doing so you'd have absolutely no control over the phase of audio frequencies contained in those signals. Phase is about time and it's about frequency: it's about the time of each single frequency of an audio signal. Tuned Mic'ing is about the control over the phase of each (with special regard to the lower portion of the audio spectrum).

I sincerely hope you are willing to try all this by yourself to understand that phase is not a problem at all... Have fun!

tunedmiking.net