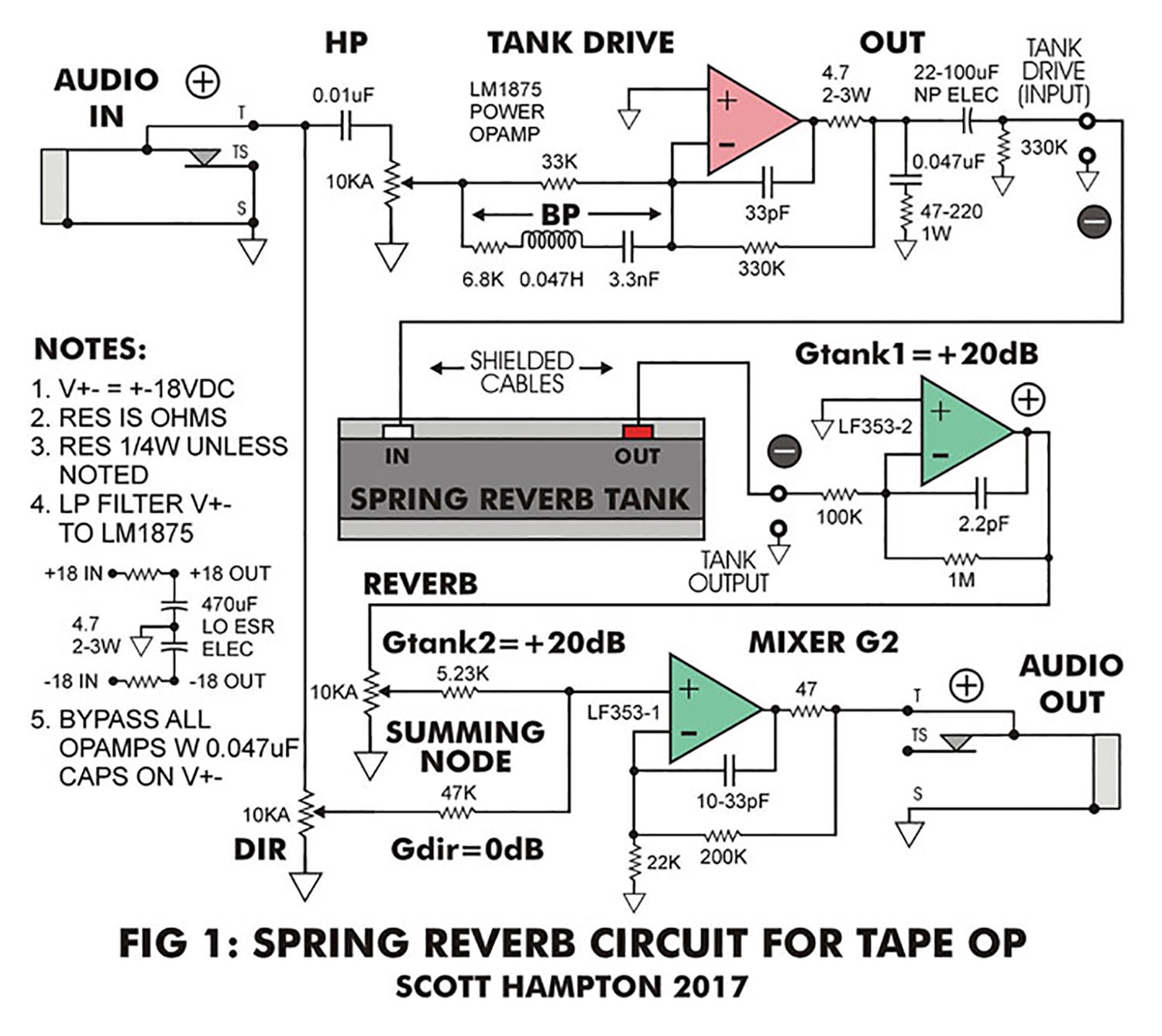
Simplified Reverb Tank Overview
A modern reverb tank consists of drivers, transmission springs, pickups, and a shock mounting system. A signal is driven into the drivers (attached to one end of each spring, labeled "input"), which acts like a speaker; but instead of moving air, it modulates the springs. The opposite end of each spring is attached to a pickup, which converts the vibration of the spring into a small current/voltage (depending on how you look at it in the circuit). Each spring has a damper disk, which does as its name implies, damping the spring to shorten the decay time and control the modulation. The pickups share a common core (similar to a transformer) so their outputs are summed. Typical tanks have two or three springs, which are usually slightly different to provide a richer, denser sound. Each transmission spring may be divided, further creating complexity in the reverb. The mechanical properties of the springs determines the decay/reverb characteristics. Tanks also have a wide range of input and output impedances.
If you are replacing one, it is important to get these as close to what the original one was in order to ensure they are driven, and amplified correctly.
Driving Reverb Tanks
Accutronics/Belton (now Accu-Bell Sound Inc.), the popular manufacturer of spring reverb tanks, states on their website, "First and foremost, the point to remember is to drive the unit as hard as practical. The core saturation level is approximately 2.5 A-T (amps measured RMS [Root-Mean-Square]). The driver, at maximum expected input level, should drive the coil to near saturation. This is of utmost importance in applications where a speaker is mounted in the same enclosure as the reverb, such as a guitar amp or organ. This will allow the output, or recovery amplifier gain, to be reduced, lowering possibilities of feedback and minimizing microphonics." Basically, they are saying you need to drive the tank hard to get maximum output. The current is limited by the power supply rails, divided by the tank Zin. Tanks with low Zin (8-16 ohms) need a lot of current, whereas tanks with a high Zin (1-3 kohms) need high voltage rails (i.e., tube amps). I've found that tanks with intermediate Zin (50-300 ohms) were a good choice for typical +-15<->24 VDC rails, where a reasonable amount of power can be delivered without either high current or high voltage power supplies.
Input Impedance
Unlike driving a speaker, the drive signal to a reverb tank is ideally not flat, with respect to frequency. Accu-Bell specifies that the signal should rise 6 dB per octave to deliver constant current over the frequency range, or to use a constant current driver circuit. This reason is due to the fact that the input impedance has both resistance and inductance, making the Zin increase linearly with respect to frequency, once the reactive part XL becomes much larger than R.
Zin = R + XL
R = DC resistance (what an ohm meter will measure)
XL = i2*PI*F*L, where "i" indicates phase angle
(i.e. imaginary)
Other parasitics (like capacitance) exist, but are omitted for simplification as they are beyond the scope of this DIY application. It is important to note the "i" term means (in this case) phase angle of 90, so the two numbers (R and XL) can't simply be added, they must be summed using vector math. The reason this is important is it will determine how much current/power you are driving the input with at the peak frequency of the drive circuit. If the tank is driven with a flat response, the drive current decreases linearly versus frequency, because Zin increases and the result is the reverb sounds dark and muddy: I = V/Zin
I spent a few days testing several tanks to see how closely the tanks behaved to the equations for Zin (R+XL). Are there parasitic impedances, or electro mechanical effects that make the input impedance change in a way different than the simple math? Using CPU-controlled test equipment (two high-resolution volt meters and a phase meter), I set up a test to measure the complex input impedance of various tanks versus frequency. I then measured the DC resistance R and inductance L using a handheld meter and mathematically calculated the Zin curves. What I found would be an article in itself, but the simple conclusion was this:
The complex Zin measured below 10-15 kHz, and those calculated from R and L measurements agreed fairly well. Some tanks deviated dramatically beyond this frequency range. Therefore, the R and L measurements from a handheld meter will yield fairly accurate predictions of how the tank is being driven relative to frequency below this range for the tanks I tested. One last comment is that the +6 dB/octave slope in the drive circuit corresponds to a constant current drive, but to deliver constant power, a +3 dB/octave slope is required. Driving with constant power has a different effect sonically, but will not be discussed here. Instead we'll be sticking to the manufacturer's recommendations.
LP and HP of the Drive Circuit
To avoid unexpected issues at low and high frequencies, it is advisable to both LP (low pass) and HP (high pass) the frequencies entering the drive circuit, in addition to the slope. Driving tanks with low frequencies generally produces unwanted rumble and distortion. Driving them up beyond 10-15 kHz or higher produces little or no usable output, so a LP in the circuit to limit the drive beyond this range is also advisable. This is important to reduce clipping the drive circuit at high frequency, i.e. continuing the boost slope beyond the practical operating range.
Constant Current Driver
The alternate way to drive a tank is by using a constant current driver circuit. I breadboarded [temporarily prototyped] three different designs based on ones offered online, as well as ones I designed, and found the following:
1. Tank dependency: Not as good for experimenting with different tanks if they have different Zin.
2. Instability: More prone to oscillating, especially with longer drive cables.
3. Noise: Feedback nature of the circuit generated more system noise in my tests.
For these reasons, mostly the first, I chose to use an amplifier with a predetermined slope and bandwidth limitation for this article. To properly design the constant current driver, the tank Zin must be known for given PSU [power supply unit] rails. Therefore, experimenting with various tanks would not be as easy. Different tanks, and short versus long, or two versus three springs, sound significantly different, so I felt having that freedom to swap out tanks was a better choice.
Output Impedance
The output impedance of a reverb tank will determine the output signal's ability to drive the makeup gain amplifier. A lower Zout will usually translate to a lower output amplitude, but higher current and lower noise susceptibility. A higher Zout will produce a bigger signal amplitude; but it can be more susceptible to noise and requires make-up gain with a higher input Z so as to not load the tank and cause undesirable effects, such as distortion and bandwidth limiting. For tanks with a 50-300 ohm Zin, the output Z is typically 1-3 kohms.
Makeup Gain
The makeup gain for a reverb tank is similar in many ways to a DI input of a microphone preamp, and you can easily use a standard DI input for experimentation. You will find, however, that an EQ after the makeup gain is very helpful in shaping the return. I tend to roll everything off below a few hundred Hz, often cutting low midrange frequencies and boosting high-end a few dB with a wide Q.
Drive
The drive circuit uses the LM1875 power amplifier. These are a great part for DIYers; they act like an op amp, except they can put out 20 W (given that you power and heatsink them adequately). They can be used for many applications, such as headphone amps, driving small speakers, and DC motor control. For this application I recommend a 5-10 W heatsink to stay in the safe area of operation (SAO) for the device. Also, they can only deliver as much power as your power supply rails, so your PSU must be chosen accordingly. The device has these added benefits over building a discrete driver circuit: power supply noise rejection, over current protection, thermal protection, low component count, simplicity to change circuit gain, easy to simulate in SPICE freeware, and it only costs $3. Some care must be taken to prevent them from oscillating at high frequencies, which is addressed in detail in the "stability" section of the data sheet (the complete data/application guide can be found at digikey.com). There are also important notes on grounding that should be adhered to. If you plan on building this, I highly recommend you read those sections of the datasheet. They are not long, nor overly technical. I built it on a breadboard, taking care to follow the power supply filtering, and had no issues. I would not recommend driving the LM1875 with a single voltage PSU, as is shown in the datasheets. It works, but it does create a massive DC surge (pop!) at power up.
The input signal is shown coming into a 1/4-inch jack, through a capacitor then a potentiometer to ground. The combination of the R & C forms a HP filter with Fc @ 1.6 kHz, and rolls off at a -6 dB/octave slope below. The output of the "Drive" control goes into the LM1875 power amp configured as an Inverting Amplifier. If you remove the "BP" components, the gain of the circuit is:

G = Rfeedback/Rin = 330 k/33 k = x10 = 20 dB (gain of an inverting op amp amplifier).
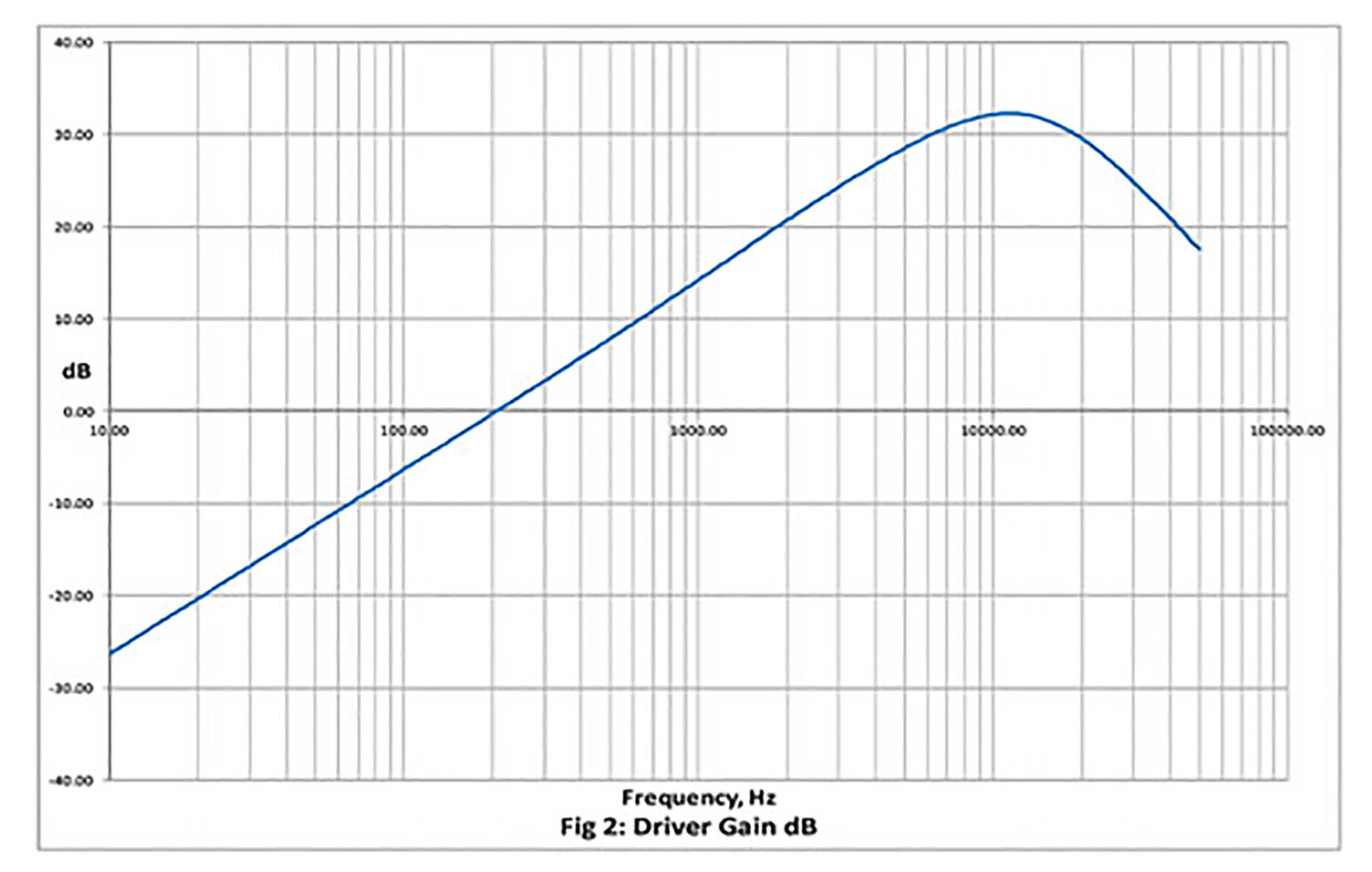
However, the "BP" circuit is in parallel with the 33 k (Rin) and will cause the circuit to act as a bandpass amplifier, with a peak around 11.5 kHz.
The impedance of the "BP" circuit at Fr (where XL=XC) goes to 6.8 k, plus the DC resistance of the inductor. As this drops, the effective "Rin" decreases causing the gain to increase. The combination of the "HP" and "BP" circuits interact, giving a good approximation of a 6 dB rise in gain per octave up to Fr; from there it begins to roll off. If you don't roll the high end off, you will limit the headroom of the drive circuit, and since driving the tanks at high frequencies produces little output, there is no benefit. The 33 pF cap further rolls off high frequency content, and helps stabilize the driver.
The 0.047 uF cap and 47-220 ohm resistor on the output is recommended in the datasheets to prevent oscillations while driving speakers. Increasing the cap value, and/or decreasing the R value, will apply more damping. I found this important, but I have reduced the amount of dampening from the datasheet because we are driving impedances in the 50-300 ohm range, not 4-8 ohms. The 4.7 ohm power resistor in the output is to protect against driving shorts, while the 22-100 uF NP (non polar) electrolytic cap prevents DC from the driver and acts as another HP. Reducing the value of it shifts its corner frequency up, i.e. cuts more low end, and the corner frequency is tank dependent.
Essentially I have reduced the drive slope filtering, as well as the power amp, into one simple circuit. Due to the simplicity of the circuit, there are a few shortcomings, like the slight shift down of the peak response with respect to the position of the "Drive" control (because the Zout of the pot changes). This can be eliminated by simply turning the drive control all the way up (or removing it and replacing it with a 10 kohm resistor to ground) and adjusting the send level. There is also a change in the input impedance of the audio input relative to both frequency and set point of the drive control. In practice this is really not an issue, as most line output devices can easily drive the circuit at its minimum value.
Make Up Gain
The entire make up gain (+40 dB for the tank), and summing with the direct signal, is done in a single dual op amp. For mine I used the common LF353 FET input dual. Audiophile grade devices can be used (like OPA27, or OPA2137), but, in practice, I found little measurable or sonic difference worth noting. The tank output goes into the first inverting amp, which has a Zin of 100 k and a gain of +20 dB. The output then drives the "REVERB" level control. The "DIR" or direct signal also goes to a volume control, then into a summing node with the reverb, where the sum of the two is amplified with another +20 dB of gain. The values of the summing resistors are different, allowing the gain of the two paths to be balanced. For this circuit, when the direct control is set to full, the direct signal has unity gain, or 0 dB. The reverb path is just slightly under +20 dB, giving the reverb signal a total of approximately +40 dB of gain.
I have not added any EQ'ing to the makeup section, however there are a couple of simple things that can be done. Adding a cap in series, with the "reverb" level control, similar to the input of the drive amp, will roll off low end, which I often find myself doing. Adding a 0.015 uF cap in series with the 100 kohm resistor on the make up gain input will also create a 105 Hz HP.
Mechanical Considerations and Noise
Because of their electromechanical design, reverb tanks are susceptible to shock and vibration. Most have an internal shock mount inside. Adding isolation grommets to the mounting screws helps too. The output section of the tank is susceptible to electromagnetic fields, so they should not be placed near power cords, power strips, and especially power transformers. In some cases, I have found adding a ground wire to the reverb tank chassis is absolutely essential. To do this you have to remove the clear (non-conductive) coating or paint (if painted) on one of the flanges, then bolt a ground lead on using one of the many spare holes. Cables leading to and from the tank should be high-quality shielded coaxial. For the best signal to noise performance, I have fabricated mu-metal shields around the "output" section of the tanks to better shield them. However, a lot of power supply filtering, power transformer shielding/isolation, and chassis shielding need to be done first to see any real benefit. Keep in mind that sheet mu-metal is expensive.
Hopefully this information will help others design and build their own, unique spring reverb units and enjoy the beauty of electromechanical reverbs.





